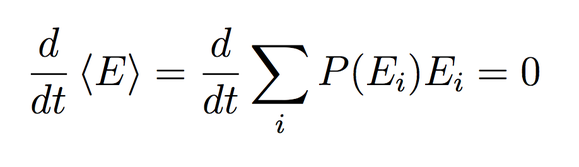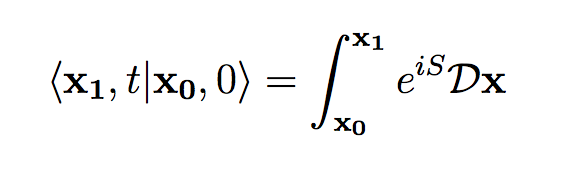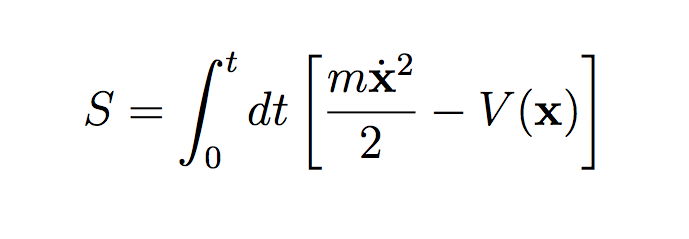Breal
There has been a problem with the multiverse theory that has bothered me for some time, the resolution of which I will present here. The problem that has bothered me is that of the conservation of energy in the multiverse. Specifically what happens when a particle tunnels through a barrier? The solution is to drop the notion of energy conservation as a local concept, one being satisfied in every branch of the multiverse, and to treat it instead as a global property of closed systems in the multiverse.
Tunneling is the phenomena that particles can escape potential wells, even when the wells are classically inescapable without sufficient energy. Consider, for instance, the case of a football placed on one side of a hill. If the football is initially stationary, or has a kinetic energy smaller than the potential energy of gravity at the highest point on the hill, then the football will not be found on the other side of the hill at some later point in time (given that no outside forces influence the football-hill system, such as by someone kicking the football).
The quantum mechanical analogue of this system does allow for the football to be found on the other side of the hill, even if the kinetic energy of the football is not great enough for the ball to roll over the hill classically. On first sight it seems like the conservation of energy has to be violated for this to be possible. So what is the mainstream resolution to this problem?
Through the Copenhagen interpretation one presumably resolves this as follows. According to the Copenhagen interpretation, the quantum-football is a wave, i.e. an object with non-zero volume with dynamics governed by the Schrödinger equation, but becomes an object with a well defined center of mass when measured. Tunneling preserves the energy because the energy of the quantum wave before measurement is conserved.
There are problems with this interpretation, one of them being that the collapse dynamics do not allow for conservation of energy; when the wave becomes localized the conservation of energy is violated. Instead, through the Many-Worlds interpretation of quantum mechanics one is able to resolve this problem comprehensibly.
In the many-worlds interpretation the quantum-football has a well-defined center of mass, as well as a well-defined trajectory in each branch* of the multiverse. In some of these branches the football is initially stationary after which it follows a trajectory such that it rolls over the hill, thereby violating the conservation of energy in that branch.
Again there seems to be a violation of the conservation of energy. Should the concept simply be dropped as a principle of quantum mechanics? The answer to this is: no, we can retain a meaningful notion of energy conservation. However, energy can no longer be thought of as a locally conserved quantity in the multiverse, i.e. not all branches satisfy energy conservation. Instead, the conservation of energy --- as well as the conservation of all other quantities in quantum mechanics --- is a global property of the multiverse: the weighted sum of the energies over the different branches of the multiverse does not change with respect to time. Mathematically this is expressed as follows.
Tunneling is the phenomena that particles can escape potential wells, even when the wells are classically inescapable without sufficient energy. Consider, for instance, the case of a football placed on one side of a hill. If the football is initially stationary, or has a kinetic energy smaller than the potential energy of gravity at the highest point on the hill, then the football will not be found on the other side of the hill at some later point in time (given that no outside forces influence the football-hill system, such as by someone kicking the football).
The quantum mechanical analogue of this system does allow for the football to be found on the other side of the hill, even if the kinetic energy of the football is not great enough for the ball to roll over the hill classically. On first sight it seems like the conservation of energy has to be violated for this to be possible. So what is the mainstream resolution to this problem?
Through the Copenhagen interpretation one presumably resolves this as follows. According to the Copenhagen interpretation, the quantum-football is a wave, i.e. an object with non-zero volume with dynamics governed by the Schrödinger equation, but becomes an object with a well defined center of mass when measured. Tunneling preserves the energy because the energy of the quantum wave before measurement is conserved.
There are problems with this interpretation, one of them being that the collapse dynamics do not allow for conservation of energy; when the wave becomes localized the conservation of energy is violated. Instead, through the Many-Worlds interpretation of quantum mechanics one is able to resolve this problem comprehensibly.
In the many-worlds interpretation the quantum-football has a well-defined center of mass, as well as a well-defined trajectory in each branch* of the multiverse. In some of these branches the football is initially stationary after which it follows a trajectory such that it rolls over the hill, thereby violating the conservation of energy in that branch.
Again there seems to be a violation of the conservation of energy. Should the concept simply be dropped as a principle of quantum mechanics? The answer to this is: no, we can retain a meaningful notion of energy conservation. However, energy can no longer be thought of as a locally conserved quantity in the multiverse, i.e. not all branches satisfy energy conservation. Instead, the conservation of energy --- as well as the conservation of all other quantities in quantum mechanics --- is a global property of the multiverse: the weighted sum of the energies over the different branches of the multiverse does not change with respect to time. Mathematically this is expressed as follows.
Here E represent the the total energy of the system, P(E_i) denotes the measure of branches with energy E_i and the sum is taken over all possible energies (labeled by the index i). P(E_i) is also the probability of measuring energy E_i.
This also makes intuitive sense. Quantum mechanics is a theory of many different universes --- or, as I have denoted them in this post, branches --- interacting with one another. In the case of the quantum-football the branches are differentiated by the different trajectories of the football. But given the initial conditions of the football there is only one path that conserves the energy of the football at every point along that path**. Thus, there is a trait off between a plurality of paths and energy conservation, which is resolved by quantum mechanics in favor of plurality.
Edit:
In the original post I did not elaborate on the origins of the plurality of quantum physics. As I said in the original post: quantum mechanics is a theory of many different branches --- or universes --- interacting with one another. But how do we build this plurality into the theory in such a way that classical theory can be taken as a limit? This is a very non-trivial question and fundamentally quantum mechanics is an answer to this question.
After writing this blogpost I realised that quantum mechanics has two main ingredients to it. Firstly, it allows almost anything to happen in single branches of the multiverse, such as, for instance, the violation of the conservation of energy. Secondly, it imposes a structure that the multiverse as a whole, i.e. all the branches taken together, must conform to.
This is most evident in the example of a quantum particle. Perviously I talked about a "quantum football" and the two are analogues, a particle being like a football with zero radius. Henceforth, when I talk about particles I will be referring to the aforementioned definition. So for the following thought experiment, let's initialise a particle it at some position x_0, after which we will wait a time t and observe the particle again. What is the probability of observing it at position x_1? This will be the question I wish to address. According to a beautiful and important formalism, called the path integral formalism, the probability of observing the particle at position x_1 at time t can be obtained by summing---or, less intuitively, integrating ---over all possible paths that connect x_1 and x_0, each path being weighted by some complex exponent. This can be expressed mathematically as follows.
This also makes intuitive sense. Quantum mechanics is a theory of many different universes --- or, as I have denoted them in this post, branches --- interacting with one another. In the case of the quantum-football the branches are differentiated by the different trajectories of the football. But given the initial conditions of the football there is only one path that conserves the energy of the football at every point along that path**. Thus, there is a trait off between a plurality of paths and energy conservation, which is resolved by quantum mechanics in favor of plurality.
Edit:
In the original post I did not elaborate on the origins of the plurality of quantum physics. As I said in the original post: quantum mechanics is a theory of many different branches --- or universes --- interacting with one another. But how do we build this plurality into the theory in such a way that classical theory can be taken as a limit? This is a very non-trivial question and fundamentally quantum mechanics is an answer to this question.
After writing this blogpost I realised that quantum mechanics has two main ingredients to it. Firstly, it allows almost anything to happen in single branches of the multiverse, such as, for instance, the violation of the conservation of energy. Secondly, it imposes a structure that the multiverse as a whole, i.e. all the branches taken together, must conform to.
This is most evident in the example of a quantum particle. Perviously I talked about a "quantum football" and the two are analogues, a particle being like a football with zero radius. Henceforth, when I talk about particles I will be referring to the aforementioned definition. So for the following thought experiment, let's initialise a particle it at some position x_0, after which we will wait a time t and observe the particle again. What is the probability of observing it at position x_1? This will be the question I wish to address. According to a beautiful and important formalism, called the path integral formalism, the probability of observing the particle at position x_1 at time t can be obtained by summing---or, less intuitively, integrating ---over all possible paths that connect x_1 and x_0, each path being weighted by some complex exponent. This can be expressed mathematically as follows.
The left-hand-side of the equation can, for our purposes, simply be read as a formal, mathematical description of the questioned I posed before (what is the probability of a particle, initialised at position x_0, time 0, to be found at position x_1, time t). The right-hand-side is the mathematical notation for the integral over all possible paths connecting x_0 and x_1, where the paths have weight exp{i S} (I'm using natural units: hbar = c = 1). The S in the exponent is not just any random function, it is called the action and it plays a very important role in classical physics: minimising the action will give Newton's equations of motion.
Note that there are barely any physical constraints; every path that connects x_0 to x_1 contributes to the probability. This gives the much needed room for the existence of different universes, but there are also enough constraints such that classical physics can emerge. This is why the weighting of the paths is so important. The details are rather technical, but in the classical limit the only path that contributes to the probability is the classical path. Thus, in this limit every observer in the multiverse is overwhelmingly likely to observer a particle following a classical trajectory.
Why is this of importance for the multiverse? Because it tells us something deep about the difference between the multiverse as a whole and the local branches of the multiverse. We see those two same ingredients that I talked about earlier. Firstly, quantum mechanics barely puts any constraints on what can happen in a single branch of the multiverse; particles can take every geometrically allowed trajectory. Secondly, there is global multiverse structure build in, the copies of the particle in different branches can interfere with one another; this interference is such that, when taking the classical limit the only path observers in the multiverse will measure is the classical path (the path one would obtain when using Newton's equations of motion).
This edit is a lot vaguer then the original post is, but I hope the thoughts explored here were enjoyable enough, or at least that the path integral formalism was fun to see :-)
*Note that these branches can also interfere with one another. The interference between branches is governed by the Schrödinger equation just as in the Copenhagen interpretation. In fact, both interpretations are mathematically nearly identical in structure.
**This is precisely why the concept of energy is so useful in classical mechanics; modulo the initial conditions, the conservation of energy fully determines the path along which a particle will travel.
Note: I expect to expand this idea somewhat further in the future, so at some point in time this post will be extended. Also, I will provide some extra links to papers and such today. (25/08/2017)
Why is this of importance for the multiverse? Because it tells us something deep about the difference between the multiverse as a whole and the local branches of the multiverse. We see those two same ingredients that I talked about earlier. Firstly, quantum mechanics barely puts any constraints on what can happen in a single branch of the multiverse; particles can take every geometrically allowed trajectory. Secondly, there is global multiverse structure build in, the copies of the particle in different branches can interfere with one another; this interference is such that, when taking the classical limit the only path observers in the multiverse will measure is the classical path (the path one would obtain when using Newton's equations of motion).
This edit is a lot vaguer then the original post is, but I hope the thoughts explored here were enjoyable enough, or at least that the path integral formalism was fun to see :-)
*Note that these branches can also interfere with one another. The interference between branches is governed by the Schrödinger equation just as in the Copenhagen interpretation. In fact, both interpretations are mathematically nearly identical in structure.
**This is precisely why the concept of energy is so useful in classical mechanics; modulo the initial conditions, the conservation of energy fully determines the path along which a particle will travel.
Note: I expect to expand this idea somewhat further in the future, so at some point in time this post will be extended. Also, I will provide some extra links to papers and such today. (25/08/2017)