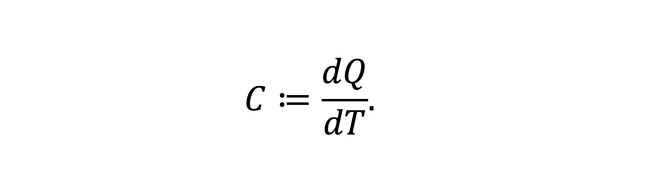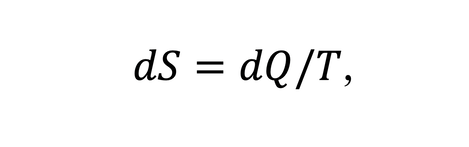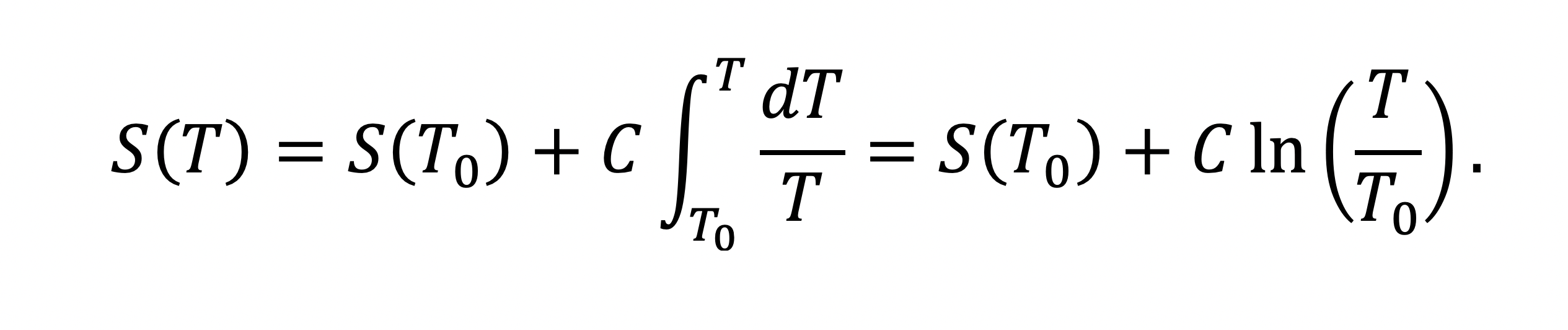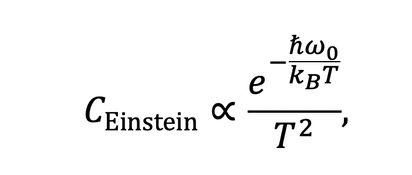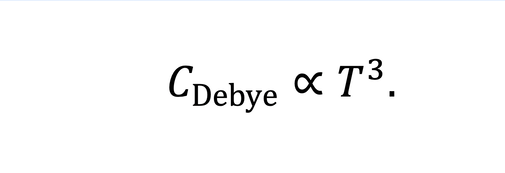Breal
A widespread misconception about quantum theory is that it only applies to small systems, such as atoms and fundamental particles. This is a falsehood: quantum theory can, with ease, describe physical systems that are of macroscopic size and often does so better than classical mechanics—perhaps unsurprisingly, as classical mechanics is false.
In fact, some of the foundational issues in classical mechanics that lead to the discovery of quantum theory were problems in solid-state physics, a branch of physics which deals with materials and their properties. And these physical systems, like gasses, metals, and liquids, are generally macroscopic.
One such fundamental problem within in the classical theory of solids and gasses revolved around heat capacity—i.e., the amount of energy required to increase the temperature of an object by one Kelvin:
In fact, some of the foundational issues in classical mechanics that lead to the discovery of quantum theory were problems in solid-state physics, a branch of physics which deals with materials and their properties. And these physical systems, like gasses, metals, and liquids, are generally macroscopic.
One such fundamental problem within in the classical theory of solids and gasses revolved around heat capacity—i.e., the amount of energy required to increase the temperature of an object by one Kelvin:
Here dQ and dT are infinitesimal changes in a system’s heat and temperature, respectively. In classical systems, the heat-capacity is independent of the temperature and violates the third law of thermodynamics, which states that a system's entropy should vanish whenever the temperature of that system approaches zero. Note that entropy is defined as
where dS is an infinitesimal change in entropy. To clarify this contradiction, integrate the expression for entropy, using the fact that the heat capacity is constant, to obtain
Thus, in the limit where T0 approaches zero, the entropy becomes arbitrarily large. So despite thermodynamics being conceived as a classical theory, meant to solve conceptual problems related to engines in the 19th, it somehow conflicted with classical mechanics. (A sign that thermodynamics is a lot deeper than its humble origins might suggest.) Heat capacity was at the core of a foundational issue in solid state physics that was only resolved with the advent of quantum theory.
Like other interesting open-problems in early 20th century physics, the problem of constant classical heat-capacity was solved by Einstein: by using quantum theory, Einstein treated each atom in a crystal as a quantum harmonic oscillator—note that crystals are useful for theoretical studies, but Einstein's results do apply to solid materials generally. In such an ideal crystal, now known as an Einstein solid, the heat capacity is temperature dependent and in the low-temperature limit becomes
Like other interesting open-problems in early 20th century physics, the problem of constant classical heat-capacity was solved by Einstein: by using quantum theory, Einstein treated each atom in a crystal as a quantum harmonic oscillator—note that crystals are useful for theoretical studies, but Einstein's results do apply to solid materials generally. In such an ideal crystal, now known as an Einstein solid, the heat capacity is temperature dependent and in the low-temperature limit becomes
such that the entropy vanishes when T goes to zero, in accordance with the third law. (This can be check by integrating the expression for entropy, using Einstein's heat capacity.) Here hbar is Planck’s reduced constant, kB is the Boltzmann constant, and omega is the characteristic frequency of the Einstein solid.
Einstein’s model was not entirely in agreement with experimental data and was later refined by Debye, who argued that a solid also contains lattice vibrations that should be considered as a kind of emergent particle—so-called quasiparticles—each of which contributes some energy to the system. Consequently, at low temperatures, the heat capacity in Debye’s model has temperature dependence
Einstein’s model was not entirely in agreement with experimental data and was later refined by Debye, who argued that a solid also contains lattice vibrations that should be considered as a kind of emergent particle—so-called quasiparticles—each of which contributes some energy to the system. Consequently, at low temperatures, the heat capacity in Debye’s model has temperature dependence
Similarly, all other properties of solids, e.g. rigidity, conductivity, and magnetisation, are explained by quantum theory; the same is true for liquids, gasses, and other states of matter. Even at large scales, quantum theory—not classical mechanics—is needed to explain the behaviour of matter; the multiverse is non-trivially different from a single-universe explanation, even for macroscopic physical systems.
Photo used under Creative Commons from timsnell